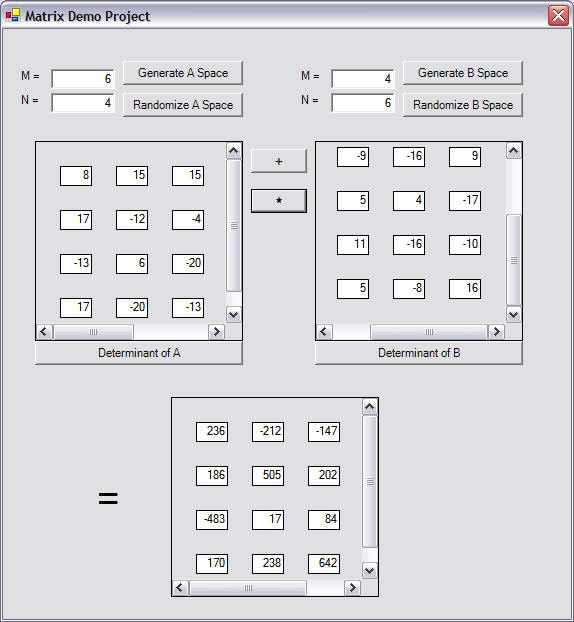
Explained with Mathematical EquationsBy Saad KhakwaniDevelopment of a Matrix class, including basic arithmetic functions and various determinant methods explained with the help of mathematical equations VB, Windows, .NET, Visual Studio, DevPosted: 14 May 2007Updated: 16 May 2007 Views: 17,919Bookmarked: 29 times Announcements Summer Code Competition! New thawte Scavenger Hunt! Monthly Competition Want a new Job? Senior Software Developer at MOC1 Solutions, LLC in United States Senior .NET Programmer/Architect at Greater Than Solutions in United States Senior Software Engineer - Server Solutions at Vital Images in United States View Latest Jobs... Chapters Desktop Development Button Controls Clipboard Combo & List Boxes Dialogs and Windows Desktop Gadgets Document / View Edit Controls Files and Folders Grid & Data Controls List Controls Menus Miscellaneous Printing Progress Controls Selection Controls Shell and IE programming Smart Client Splitter Windows Static & Panel Controls Status Bar Tabs & Property Pages Toolbars & Docking windows Tree Controls Web Development Ajax and Atlas Applications & Tools ASP ASP.NET ASP.NET Controls ATL Server Caching Charts, Graphs and Images Client side scripting Custom Controls HTML / CSS Internet / Network ISAPI Site & Server Management Session State Silverlight Trace and Logs User Controls Validation View State WAP / WML Web Security Web Services Enterprise Systems Content Management Server Microsoft BizTalk Server Microsoft Exchange Office Development SharePoint Server Multimedia Audio and Video DirectX GDI GDI+ General Graphics OpenGL Database Database SQL Reporting Services Platforms, Frameworks & Libraries ATL MFC STL WTL COM / COM+ .NET Framework Win32/64 SDK & OS Vista API Vista Security Cross Platform Game Development Mobile Development Windows CardSpace Windows Communication Foundation Windows Presentation Foundation Windows Workflow Foundation Libraries Windows Powershell LINQ Languages C / C++ Language C++ / CLI C# MSIL VBScript VB.NET VB6 Interop Other .NET Languages XML Java General Programming Algorithms & Recipes Bugs & Workarounds Collections Cryptography & Security Date and Time DLLs & Assemblies Exception Handling Localisation Macros and Add-ins Programming Tips String handling Threads, Processes & IPC WinHelp / HTMLHelp Graphics / Design Expression Usability Development Lifecycle Debug Tips Design and Architecture Installation Work Issues Code Generation General Reading Book Chapters Book Reviews Hardware Reviews Interviews Scrapbook Hardware & System Third Party Products Product Showcase Solution Center Services Job Board Code Project Coffee Free Magazines Feature Zones Product Showcase IBM DeveloperWorks WhitePapers / Webcasts Quest SQL Zone InstallShield 2009 Search   Articles Messages Jobs   Advanced SearchSitemap | Add to IE Search Print   Report Article   Watch   Bookmark   Discuss    Send to a friend 9 votes for this Article. Popularity: 4.12 Rating: 4.31 out of 5 1 2 3 4 5 Download demo project - 9.1 KB Download source - 1.6 KB Introduction There are many sources available on the internet which provide different implementations of Matrices. My idea here is not only to develop a Matrix class but to take a systematic approach to programming such types of problems with the aid of mathematical equations. This Matrix class is not complete by any means, but it is accompanied with complete documentation. Matrices find many important applications in different fields of science and are used to describe linear equations. They contain coefficients of linear transformations and can be added, multiplied, and decomposed in various ways. This marks them as a key concept in linear algebra and matrix theory. They are of so much importance in the sciences and mathematics that they are the building blocks of many commercial software applications, like MATLAB. This article deals with the development of a Matrix class using VB.NET. Every function that will be coded will be preceded by a formal mathematical definition of the function. Background A matrix is a rectangular array of numbers. More generally, it can be a two-dimensional array of quantities which can be algebraically operated upon. In general terms, these "quantities" may be any abstract entities that can be added or multiplied -- for example, integers, fractions, polynomials, etc -- but in this article we consider a simple case by using Double as these quantities. Developing the code A matrix A can be organized as: The standard in which we choose to represent a matrix is not a big issue here for us. Some information follows: As for a standard representation of matrices, we can identify a single element ai,j as the element at the ith row and jth column. However, if we are considering the horizontal axis as x and the vertical as y, then according to the above organization ai,j is the element located at x=i and y=j, which will be the same element as aj,i if the convention of row and column were to be followed (note the reversed subscripts). In other words, x=i represents a column not a row, but x runs through a row (x=0 represents 0th column, x=1 represents 1st column, and so on, but x is running through a row). The 2-dimensional space in both mathematics and in computer languages is specified as the second representation. Hence it is chosen for our purposes, and we can proceed by declaring our class: Public Class Matrix Implements ICloneable Private M As Integer ' Horizontal Size = No. of Columns Private N As Integer ' Vertical Size = No. of Rows Public val(,) As Double Private currentX As Integer Private currentY As Integer End Class Here, val(,) is a two dimensional array containing the elements of the matrix. In the constructor of the class, we need to assign proper dimensions to our matrix: Public Sub New(ByVal X As Integer, ByVal Y As Integer) SetDimensions(X, Y) currentX = 0 currentY = 0 End Sub Public Sub New(ByVal X As Integer) SetDimensions(X, X) currentX = 0 currentY = 0 End Sub Private Function SetDimensions(ByVal X As Integer, ByVal Y As Integer) M = X N = Y ReDim val(M - 1, N - 1) End Function The constructor is overloaded, one for a rectangular matrix case and the other for a more specific square matrix case. Note here that since our 2-dimensional array is zero-based, if M is the horizontal count then the elements are indexed 0 to M-1. Matrix addition Now, we are going to add a function to our class which will receive another matrix and do element-by-element addition. If C is the matrix added to matrix A to obtain matrix B then: for all i and j. In other words: and Also, the dimensions of A and C must match. Public Function Add(ByVal C As Matrix) As Matrix If M <> C.M Or N <> C.N Then Throw New Exception("Matrices size Mismatch.") End If Dim B As Matrix = New Matrix(M, N) For i As Integer = 0 To M - 1 For j As Integer = 0 To N - 1 B.val(i, j) = val(i, j) + C.val(i, j) Next Next Return B End Function Matrix multiplication Now we move ahead to program the multiplication function. Multiplication can only be performed on two matrices if the number of columns (M) of first is equal to the number of rows (N) of the second. In other words, if matrix A and C are to be multiplied then for B=AC, according to our variables, this is only possible if A.M = C.N So: Public Function Multiply(ByVal C As Matrix) As Matrix If M <> C.N Then Throw New Exception("Matrices size Mismatch.") End If ... ... End Function Remembering the matrix multiplication as follows: So, If B=AC, a complete row of A (e.g. 0th row is [1 0 2] in the above example) can be addressed as A.val(i,J) where i is the index to access individual element in a row and j=J will be a constant (j=J=0 for the 0th row case). Similarly, a complete column of matrix C is specified as C.val(I,j). In order to carry out the multiplication, we note that there is a one-to-one correspondence between running indices i and j. Thus, we write i=j=k. The first element of the resultant matrix B, B.val(0,0), can be found by summing the products [A.val(k,0) and C.val(0,k)] over all k: Generally, for any element at (i, j) in matrix B: where and Dim B As Matrix = New Matrix(N, C.M) For j As Integer = 0 To N - 1 For i As Integer = 0 To C.M - 1 For k As Integer = 0 To M - 1 ' or 0 to C.N -1 B.val(i, j) += val(k, j) * C.val(i, k) Next Next Next Return B Matrix determinant There are many ways by which the determinant of a matrix can be obtained. The most popular is expansion by a specific column or a row. Others are Gauss–Jordan elimination, and Gaussian elimination. Expansion by a row/column Expanding by a specific row or a column is the simplest method and it will be used first to program the problem. For all those who have forgotten or don't know this method, consider the calculation of the determinant of the following matrix, expanding by the 0th row: then where comes from the original matrix A by cutting out 0th row and 0th column. Note +1, -2 and +3 -- the sign alternates between positive and negative. Looking at the above step, it can be seen that the problem of calculating the determinant of this single 3x3 matrix is reduced to a problem of calculating the determinants of three 2x2 matrices. If the original matrix is of 4x4 size then after expanding by the 0th row, four 3x3 matrices are obtained. Then for each of those four, repeating the same procedure would have produced three 2x2 matrices, resulting in an ultimate total of twelve 2x2 matrices. Continuing the same procedure on these 2x2 matrices would have yielded twenty-four 1x1 matrices. To program this procedure, first consider a function SubMatrix(x, y) which generates a matrix S from the original matrix, having row y and column x cut out. This can be expressed as: is the operator for adding an element into the matrix, just as summation is the operator for the arithmetic addition for the numbers. First, we program a procedure which adds an element val(i,j) to the matrix S, filling out rows first. Public Function AddElement(ByVal element As Double) If currentX > (M - 1) Then currentY += 1 currentX = 0 End If Try val(currentX, currentY) = element Catch e As Exception Throw New Exception("Matrix filled with values.") End Try currentX += 1 End Function The resultant matrix should not contain the elements from the matrix A, which appear in the yth row and xth column. For example, if: then SubMatrix(2,1) will give: or Public Function SubMatrix(ByVal x As Integer, ByVal y As Integer) As Matrix Dim S As Matrix = New Matrix(M - 1, N - 1) For j As Integer = 0 To N - 1 For i As Integer = 0 To M - 1 If (i <> x And j <> y) Then S.AddElement(val(i, j)) End If Next Next Return S End Function After the definition of SubMatrix(x,y), we may easily derive the recurrence relation from the above procedure: for and Every recursive procedure has a base case. The base case for val(0,0)above uses the fact that the only element that is in a matrix of size is 1x1 is the determinant of that matrix. Public Function Determinant() As Double If M = 1 And N = 1 Then Return val(0, 0) End If Dim temp As Double Dim MySubMatrix As Matrix Dim j As Integer = 0 For i As Integer = 0 To M - 1 MySubMatrix = SubMatrix(i, j) temp += ((-1) ^ (i + j) * val(i, j) * MySubMatrix.Determinant()) Next Return temp End Function For all those who want to relate this to theory and standard definitions like Minor and Cofactor, please note:det(SubMatrix(i,j)) is a minor M(i,j) of the matrix A and the cofactor C(i,j) of A is defined as (−1)i + j times the minor M(i,j) of A. Then it can be readily seen that the above equation is a specific form of Laplace's formula along the row j, when j = 0. Gaussian elimination This method is not conducive to good programming as it is factorial order, i.e. O(n!). Its utility is thus greatly reduced for larger values of n, in that it would take a lot of time to execute. To avoid this, we make use of some of the properties of matrices. One is very important here, stating: Multiplying one complete row or column of a matrix with a constant and subtracting the resulting column from another row or column would not change the determinant of the matrix. By proper manipulation of a matrix, we can make all of the elements but one equal to zero in any row. In this case, let j=Y be a constant row. From here, we need to expand the matrix. Let us define k as the first non-zero element in the row Y, where we must let Y be 0: Dim Y As Integer = 0 Dim k As Integer For i As Integer = 0 To M - 1 If val(i, Y) <> 0 Then k = i Exit For End If Next Now we take this non-zero element val(k,Y) and try to make all of the other elements of the row Y equal to zero. This can be done with the use of a property and can be best understood with an example. Let: Here, take Y = 0. Then k = 1, as the element val(1,0) = 2 is the first non-zero element in the row Y = 0. Now we analyze this complete row. We want all of the elements of this row except one to be zero. So, by using the middle column, we can make the top elements of all the other columns equal to zero (element 3 in this case). In other words, columns i = k + 1 onwards are required to be made zero, since for j < k the elements are already zero. By the use of the property, we multiply the column headed by 2 with (2/3). This will transform the matrix as: Note the inequality above. Now according to the property, the middle column can be subtracted from the last one to restore A. Thus: Note here that the middle column is not changed; it remains as what the original was. Expanding by the 0th row yields: Here, since all the other elements in the first row except one are zero, a matrix of 3x3 thus yielded only one 2x2 matrix. This is a big improvement over the previous method, where one nxn matrix yielded n number of (n-1xn-1) matrices. In contrast, this method always produces one (n-1xn-1) matrix from an nxn matrix. To put this complete procedure mathematically -- and thus "programmatically" -- we write: for all and Of course, if the top element of a column is already zero, we don't waste time making it zero again. So check for val(i,Y) = 0. Dim f As Double For i As Integer = k + 1 To M - 1 If val(i, Y) <> 0 Then f = val(i, Y) / val(k, Y) For j As Integer = 0 To N - 1 NewMatrix.val(i, j) = val(i, j) - val(k, j) * f Next End If Next Here, is a factor declared as double. We have written NewMatrix.val(i,j) = . . . in the above code, rather than val(i,j) = . . . This is a little memory conservation step and is explained as follows. In the crude expansion by a row method, we took out one element from a particular row, generated the SubMatrix and then we did the same to the newly formed matrix. We didn't throw away the old matrix after the formation of a new matrix through SubMatrix because there were other elements of that same row awaiting their turn in the old matrix. In this method, however, we can easily throw away the old matrix once a SubMatrix is formed because there is no awaiting element. This is because all of them are zero. It is important that we don't throw away the original matrix, though, because the determinant method is not intended to change the contents of the matrix on which it is called. It can do whatever it wants to the matrices or submatrices that it creates itself, however, so the method's signature is: Private Function GEDeterminant(ByVal DoClone As Boolean) As Double If M = 1 And N = 1 Then Return val(0, 0) End If Dim NewMatrix As Matrix If DoClone Then NewMatrix = Clone() Else NewMatrix = Me End If ... End Function Now we use: NewMatrix = NewMatrix.SubMatrix(k, Y) 'Save space temp += ((-1) ^ (k + Y)) * val(k, Y) * NewMatrix.GEDeterminant(False) Return temp Where temp was declared as a temporary variable earlier via: Dim temp As Double Clone() can be easily programmed as: Public Overridable Function Clone() As Object Implements ICloneable.Clone Dim temp As Matrix = New Matrix(M, N) temp.val = val.Clone Return temp End Function The Public function is of the form, since we need to Clone() the original matrix: Public Function GEDeterminant() As Double If IsSquare() Then Return GEDeterminant(True) Else Throw New Exception("Determinant exists only possible" & _ "for a sqaure matrix.") End If End Function Finally: Public Overrides Function ToString() As String Dim temp As String For Y As Integer = 0 To N - 1 For X As Integer = 0 To M - 1 temp &= val(X, Y) & "," Next X temp &= Chr(13) Next Y Return temp End Function Points of interest One interesting thing is that, while programming the GEDeterminant() method, I didn't know that it was called the Gaussian elimination method. Expansion by a row was just not practical enough. For example, the O(n!) determinant of a 10x10 matrix caused delays on the order of tens of seconds, whereas a delay of only 200 ms was experienced for the one thousand 10x10 matrices in the Gaussian elimination method O(n3). This Matrix Class has helped me solve many problems in varying fields. Use of Crammer's Rule to find the solution of simultaneous linear equations is one such important use of matrices. Remember that I used the phrase, "abstract entities that can be added or multiplied," earlier in the article. For this article we used Double as an abstract entity, but the use of a self-defined Polynomial can ease our way to the solution of complex electrical circuits -- like SPICE does -- using modified nodal analysis. Another important application of matrices that I have used extensively is to approximate a polynomial function from any number of given samples. The approximations can generally be in any form, including exponential, sinusoidal etc. Approximations in the form of sinusoids lead to the formation of Fourier Series -- both continuous and discrete -- and thus a whole new world of exploration. History 14 May, 2007 - Original version posted License This article has no explicit license attached to it but may contain usage terms in the article text or the download files themselves. If in doubt please contact the author via the discussion board below. A list of licenses authors might use can be found here About the Author

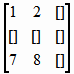
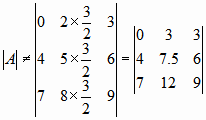
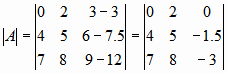
评论