标 题: 【原创】CRC技术的实现与破解(10.21更新)
发帖人:vipchenji
时 间: 2005-09-26 16:23
原文链接:http://bbs.pediy.com/showthread.php?threadid=17195
详细信息:
这是一个已经发表的文章,用于普及知识,今天冒昧放上,请各位点评!
上次发的是全文字版,经过修改,再发一次图文版(注:完整图文版请到上面的原谅链接页面下载)
其中参考了看雪学院中的一些精华,再次也向各位致敬!
CRC 在软件加密保护中的应用
或名(用CRC 打造软件的外衣)
注:本文相关图片没收录,带图PDF格式请到这下载:http://bbs.pediy.com/showthread.php?s=&threadid=17195
CRC(CyclicRedundancyCheck,直译:循环冗余校验)技术是一项很成熟的技术,在众多领域有广泛的应用,在数据存储和通信传输应用中处处都可以看到它的身影。最常用的CRC
校验形式有CRC-16,CRC-32两种形式,采用CRC-16校验,可以保证在1014 位码元中只含有一位未被检测出的错误,采用CRC-32校验的出错概率比CRC-16还低105 倍。CRC的主要特点
就是:检错能力极强,开销很小,易于实现。从性能和开销上综合考虑,其远远优于奇偶校验及算术和校验等方式。因此,很多软件在加密保护时都将CRC技术应用其中。本文拟从
CRC校验的原理解剖入手,用实际代码和应用给大家解析CRC校验在软件加密中的实际应用,希望能给您的软件加密保护提供一些帮助和建议。
CRC 校验的原理解析
在实际应用中,根据环境和需求的变化,CRC形成了多种变形方式。比如:通讯协议X.25的帧检错序列采用的是CRC-CCITT方式,ARJ、LHA、ZIP等压缩软件采用的是CRC-32方式,磁
盘驱动器的读写采用的是CRC-16方式,GIF、TIFF等图像存储格式也使用CRC作为检错技术。目前,比较流行的CRC形式主要是:CRC-16(CRC-CCITT)、CRC-32两种,CRC-4、CRC-8
、CRC-12等形式的应用比较少见。其实,虽然有这么多种变形方式,但其原理是完全相同的,只是在实现上有一点变化而已,下面我们就对其原理进行一番解剖,希求通透。
CRC的算法本质是(模-2)除法的余数运算,使用的除数不同,CRC的类型也就不一样。怎么样,不好理解吧?没关系,我们继续讲解:CRC的算法其实是采用了多项式编码的方法,您
可以将要被处理的数据块M看成一个n阶的二进制多项式,其形式如下:
a 是对应的阶数(位数)的值;
x是对应的“模(进制)”数,由于我们处理的都是二进制数,所以x就是2 了。(模-2)的意思现在您明白了吧?
下面我们用一个数进行解释吧:
有一个二进制数M=10010101,其对应的多项式就可以表示为:
CRC校验就是基于这种多项式进行的运算,其乘除法运算过程与普通代数多项式的乘除法相同,其加减法运算以2为模,加减时不进(借)位,实际上与逻辑异或(XOR)运算是一致
的。
通常,根据多项表达(运算)式的不同,就形成了不同的CRC形式,以下是各种常用的多项表达(运算)式:
这些多项表达式的值就是(模-2)除法的除数,只要能确定使用哪一种多项式(也就是对应除数),您就可以很简单的获取CRC检验码了。下面就给您介绍CRC检验码的计算过程(看
起来麻烦,其实简单):
1、先确定您要使用的CRC校验形式,以此确定对应除数(用G来表示)和选定阶数(用r来表示)。(如果选择CRC-4的话,r就等于4,选择CRC-16话,r就等于16,以此类推。)
2、在待处理的数据块M'后附加上r个0。假设原始数据块的长度是m位的话,附加之后的长度就变成m+r位了,我们用M来代表附加后的值。
3、用第一步选择的生成多项式的值(即对应除数G)来除第二步附加0后生成的值(M),循环计算,一直到余数的阶数小于等于r-1,这时所得到的余数(用Y表示)就是原始数据
M'经过所选择的CRC校验形式所生成的CRC校验码。
●如果您想将生成的校验码与原始数据进行复合,只需要用第二步生成的(M)以模2的方法减去得到的CRC校验码(Y),所得到的值就是包含了CRC校验码的数据串M''。(不过在
软件加密过程中可能用不到这一步)。
怎么样,很简单吧,只需要三步,就可以得到CRC 的校验码。还不明白?举个例子吧:
设原始数据M'=1100110100
选择CRC-4的形式,则G=24+2+1=19=10011(二进制)
r =G 的二进制位数减1=5-1=4
对原始数据M'进行处理,在其尾部附加r个0,即:
M=M'+0000=11001101000000
再用G 循环除M:
其实校验码生成的过程就是一个循环移位的运算,位与位之间就是异或(XOR)运算。
◆一个数据的校验过程是这样的,如果有大量数据(比如说一个可执行程序或一个压缩包)将如何进行校验呢?其实很简单,只要将一个文件看成一个被一些数字分割的很长的位
字串就可以了,只是这个位字串比较TA而已,你只要按标准的方式对这个比较长的位字串进行(模-2)除法运算,就一定会得到一个余数---CRC校验码,而这个校验码就是这个文件
的CRC校验值。
CRC 校验的代码实现
好了,理论上的准备是很多了,现在要用进入实践了。下面,我们将给您提供一段很简单而实用的代码,用来实现CRC-32校验,最终,我会用这段代码实现软件加密保护。
大家可以看到,上面生成CRC校验码的过程中,使用了大量的位运算和逻辑操作。而我想告诉大家的是,基于位运算的算法是非常慢的而且效率很低。因此,在实际使用中不推荐使
用“计算法”来生成CRC校验码,而建议使用“查表法”来进行CRC校验码计算。查表法又是什么方法呢?这里我不做过多的分析,简单的说,它是利用预先计算出的标准码表(对
应不同的校验形式有不同的码表,见附表1、2),用简单的移位和XOR操作,快速计算出CRC校验码的方法。
具体的算法就是:
(1)将上次计算出的CRC校验码右移一个字节;
(2)将移出的这个字节与新的要校验的字节进行XOR 运算;
(3)用运算出的值在预先生成码表中进行索引,获取对应的值(称为余式);
(4)用获取的值与第(1)步右移后的值进行XOR 运算;
(5)如果要校验的数据已经处理完,则第(4)步的结果就是最终的CRC校验码。如果还有数据要进行处理,则再转到第(1)步运行。
看上面的过程是十分简单的,不好理解的可能是“预先生成的码表”。其实这个码表就是2^8 的数组,为什么是8次方呢?因为我们是用字节来进行运算的,而一个字节是8位,所
以就是2的8次方了。因此这个码表就是拥有256值的数组,对应的每个值实际上就是0-255以对应的CRC多项表达式(见原理分析)为权的CRC码。如CRC-16的多项表达式就是,CRC-32的多项表达式就是:
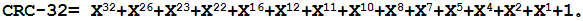
附表1、2中分别给出了对应两种形式的码表(汇编格式),您只要复制到您的代码中即可使用(可能要做一些修饰)。
如果您不想将这么一大堆码表复制到您的代码中,也可以使用动态生成码表(不过是给256个数字进行CRC计算而已)。下面是生成CRC-32码表的代码(c语言):
//--------------------------------------
//GenCrc32Tbl函数动态生成CRC-32的预置码表
//Code:Chenji
//--------------------------------------
unsignedintCRC.//在Windows下编程,int的大小是32位
unsignedintCRC_32_Tbl[256].//用来保存码表
voidGenCrc32Tbl()
{
for(inti=0.i<256.++i){//用++i以提高效率
CRC=i;
for(intj=0.j<8.++j)
{//这个循环实际上就是用"计算法"来求取CRC的校验码
if(CRC&1)
CRC=(CRC>>1)^0xEDB88320;
else //0xEDB88320就是CRC-32多项表达式的值
CRC>>=1;
}
CRC_32_Tbl[i]=CRC.
}
}
//-------------------------------------------------
●上面的代码其实就已经实现了用“计算法”求取CRC校验码的过程,只要做些修改就可以完全实现。您只要将上面的代码复制到程序中,并调用GenCrc32Tbl函数,就可以在
CRC_32_Tbl中生成CRC-32的预置码表。有了码表,用“查表法”计算CRC-32计算校验码就易如反掌了。根据上面介绍的算法,用C语言只需要一行就可以实现。
CRC32=CRC_32_Tbl[(CRC32^((unsigned__int8*)p)[i])&0xff]^(CRC32>>8);
怎么样?简单吧。
下面是完整的一个实现函数,更加简单:
//--------------------------------------------
//CalcCRC32函数计算出给定数据串的CRC-32校验码
//Code : Chenji
//--------------------------------------------
unsigned int CalcCRC32(void *DataBuff,unsigned int BufLen)
{//DataBuff是指向数据串的指针,BufLen是数据串的长度
unsigned int CRC32=0xffffffff; //设置初始值
for(unsigned long i=0; i<BufLen; ++i)
CRC32 = CRC_32_Tbl[(CRC32^((unsigned __int8 *)DataBuff)[i]) & 0xff] ^ (CRC32>>8);
//如果你的编译器不支持unsigned __int8定义,请试用unsigned char
return CRC32;
}
//-----------------------------------------------------
怎么样,用查表法计算CRC校验码是不是很简单,很快捷?您只要将上面的代码复制您的程序中,赋与对应的参数,就可以实现CRC-32校验了。还等什么,马上开始现实之旅。
CRC 校验在软件加密保护中的攻与防
上面用大篇幅介绍CRC的原理与实现,都是为现在的实战打基础,现在我们就要用实战来校验了。
大家已经知道,CRC校验生成的结果只是一个Long型的整数,市面上一些软件是如何将这个整数应用在软件加密保护中呢?这里我给大家介绍两种常用的方式:
1、是对程序自身的进行保护。首先对原始可执行程序进行CRC校验,同时保存校验结果(可以保存在注册表、配置文件或可执行程序本身)。在程序运行时,对程序自身进行CRC校
验,并将运算出的结果与保存的原始结果进行比较,如果不相同,就说明程序已经被修改(最有可能是被破解或被病毒感染)。即使只有1Bit的修改,都会被CRC检查出来,所以用
CRC做自校验相当有效。
2、用CRC校验算法,对注册名和注册码进行变形运算和判断,以此做为注册保护和授权的手段。
这两种方式在软件保护上的运用十分广泛。可以说,每一种软件加壳(加密)保护软件(如upx,Aspack,FSG等)都使用了CRC进行自身校验保护。
为了证明CRC在软件加密保护上的效果,我制作了一套测试用例,大家可以在http://www.xxx.com上下载CRCTest.rar压缩包,按本文进行测试和分析。
压缩包中有两个可执行程序:crctest.exe和Makecrc.exe。其中crctest.exe就是我们要进行分析的对象,界面如下:
软件已经进行了CRC外壳校验保护,同时,使用CRC-32算法做注册码校验,可以说将CRC在软件加密保护上的应用全部发挥出来了。
MakeCrc.exe是配套工具,用来给上面的程序注入CRC保护码和计算注册码。
现在,可以打开crctest.exe 文件,并随意输入注册名和注册码,看一看!
您也可以用16进制编辑器(如:Hiew,010Editor,RTA等),将crctest.exe的最后一个字节00修改成0F
保存修改后,再运行程序,程序会提示被修改。
怎么样,这就是CRC保护的效果。如果您试图强行暴破来完成注册的话,就必须修改原始文件,但是软件将会在自校验时发现自己被修改了,然后自动退出。除非您得到正确的注册
码或注册算法,而软件使用的注册算法也是由CRC算法变形实现的。如果在不知道具体算法的情况,想要强行暴破是比较麻烦的,这就是CRC的威力。市面上大多数软件大多是这样
做的,毕竟谁也不想自己的软件被人破解或修改,难道您不这么认为吗?
但是现在,我们就要挑战这个难题,在不了解注册算法的情况,如何实现强行暴破,彻底攻破CRC 的保护。这可能是您最希望了解的,还等什么,开始吧!
首先,您要准备一些工具:Ollydbg1.10、DeDe、Peid全能插件版,也许还需要PE-tools1.50。这些软件您可以在网上很轻松的找到,如果没有可以与我联系。
第一步:检查
Peid是目前最流行,也是比较完善的检测软件。可以检测软件是否加壳,使用了什么编译器等诸多信息,同时其丰富的插件可以完成许多扩展功能。现在,我们先用Peid检测
crctest.exe,查看程序的基本信息。Peid显示软件是用“BorlandC++1999”版的编译器进行编译的,其实一般情况下,用BCB编译的程序也会显示为用“BorlandC++1999”编译。
我们再用其中的插件“KryptoANALyzer”,来分析程序中是否有通用的加密算法。我们可以看到,程序使用了CRC-32 算法:
◆这里想告诉大家的是,KryptoANALyzer是使用查询数组(码表)来确定软件使用了什么算法,而软件使用动态生成数组(码表)的话,它是无法检测出算法来的。呵呵,这也是
它的漏洞了。你可以程序中保存一个其它算法的码表来混淆检测器。(crctest.exe中就定义了一个CRC32的数组,但我们并没有使用它,而是使用了动态生成的码表)
第二步:分析
了解软件没有加壳,而且可能是由BCB编译的之后,我们就要着手分析了。针对Borland公司出品的Delphi和BCB编译器所生成执行程序,可以使用DeDe反编译器进行分析,它可以很
好的恢复程序的原始代码信息。
下面就是用DeDe将crctest.exe载入分析,现在我们切换到“过程”页面,选择“main”单元:btn_OKClick事件是我们感兴趣的地方,当按下“注册”按钮时,这个事件会被调用
。双击这个事件,我们就可以看到这个事件的汇编代码,在其中显示的汇编代码已经被DeDe 处理过,对标准的函数调用已经进行了注释,其可读性很好。00401C90这个地址就是这
个事件函数的入口点,如果您有一些基本功,可以认真分析一下。您也许可以看出关键的代码。不过,下面我们要进入动态调试了!
第三步:调试破解
在检测和分析的基础上,我们可以开始动态调试了。我要用动态的数据来解释破解的思路与过程。现在,请打开Ollydbg动态调试器,将crctest.exe载入,停在程序的入口处。
按Ctrl+G,输入00401C90,直接定位到“注册”按钮的点击事件函数入口处,并按F2下断点。
接下来,可以按F9运行程序,进入调试,然后在窗口中,随便输入注册名和注册码,点击“注册”按钮,程序将会中断在00401C90处:不断按F8单步运行,其间您可以看到许多的
数据在变化,不用管它,一直按F8运行,直到显示注册错误的信息框,再看运行的状态。
可以看到,在运行00401FDF这个地址的时候,软件显示了注册错误的信息框。显然这个call00468C08指令就是显示信息框的函数。我们只要找到调用这个
Call的调用(有点绕舌),就可以找到关键点了。大家向上回溯代码可以看到下面的内容:我们将汇编代码提取出来如下:
===========================
/*401F65*/ lea edx,[local.2]
/*401F68*/ lea eax,[local.4]
/*401F6B*/ call crctest.00468DA0 // 对比注册码是否正确
/*401F70*/ test al, al
/*401F72*/ je shortcrctest.00401FC7//如果不正确就跳走
/*401F74*/ mov eax,dwordptrds:[46EF94]
/*401F79*/ push 40040
/*401F7E*/ lea ecx,dwordptrds:[edi+141]
/*401F84*/ lea edx,dwordptrds:[edi+EB]
/*401F8A*/ mov eax,dwordptrds:[eax]
/*401F8C*/ call crctest.00468C08 // 显示成功注册的提示信息
/*401F91*/ mov wordptrds:[ebx+10],8C
/*401F97*/ lea edx,dwordptrds:[edi+146]
/*401F9D*/ lea eax,[local.14]
/*401FA0*/ call crctest.00468C18
/*401FA5*/ inc dwordptrds:[ebx+1C]
/*401FA8*/ mov edx,dwordptrds:[eax]
/*401FAA*/ mov eax,dwordptrds:[esi+2F8]
/*401FB0*/ call crctest.00452658
/*401FB5*/ dec dwordptrds:[ebx+1C]
/*401FB8*/ lea eax,[local.14]
/*401FBB*/ mov edx, 2
/*401FC0*/ call crctest.00468CD0
/*401FC5*/ jmp shortcrctest.00401FE4
/*401FC7*/ mov eax,dwordptrds:[46EF94]//跳转到这里
/*401FCC*/ push 40010
/*401FD1*/ lea ecx,dwordptrds:[edi+1B4]
/*401FD7*/ lea edx,dwordptrds:[edi+16A]
/*401FDD*/ mov eax,dwordptrds:[eax]
/*401FDF*/ call crctest.00468C08 // 显示错误注册的提示信息
===========================
由此可以看到软件的注册检查是很简单的,只要将00401F72 处的代码:
jeshortcrctest.00401FC7
修改为:
nopnop
就可以暴破了!大家可以在Ollydbg中将00401F72处的代码修改成下面的形式:
然后,取消所有的断点,直接按F9运行程序,再随意输入注册名和注册码,点击“注册”。看到了吗?
软件已经成功注册了!但是真的成功了吗?不要高兴的太早,还有CRC自校验没有解决呢!请先将修改过的程序保存为另一个文件crctest_1.exe。
●方法:在汇编代码上点右键,选择“复制到可执行程序”--“所有改动”,再选择“全部复制”打开新的窗口。在新的窗口中点右键,选择“保存文件”,输入文件名就可以保
存。
现在,请暂时关闭ollydbg,运行新保存的文件crctest_1.exe。怎么样,没有成功吧!软件发现自己被修改了。目前,我们只完成了注册码校验的暴破,还没有解决CRC 的校验保
护,这才是我们的重头戏,而这其实很简单。马上动手!
再次打开ollydbg,这次就要载入crctest_1.exe了,因为它已经暴破了注册校验的部分。在开始之前,我们要分析一下思路:软件要进行自校验,就一定要读文件到内存中,我们
只要找到读文件的函数,就可以顺藤摸瓜找到校验的核心部分了。好,在ollydbg中按ctrl+n打开函数导入导出表,找到ReadFile函数。在ReadFile这一行上点右键,选择“在每个
参考上设置断点”,状态条上显示有六个断点被设置。不管它了,按F9开始运行!很快软件就被断下来:
大家不用花时间在这些汇编代码上,我们的目标是关键跳转点。一直按F8返回到上级调用:
最终我们会返回到00401A8B 这个地址,而在其上、下方有两个调用:
/*401A86*/ call crctest_.00401B8C //计算当前的CRC校验码
/*401A8B*/ mov esi,eax
/*401A8D*/ mov eax,ebx
/*401A8F*/ call crctest_.00401AA0 //读取原始的CRC校验码
这两个调用分别返回当前的CRC校验码和原始的CRC校验码,具体过程大家可以进入其中进行分析,这里不做详解。接下来,继续按F8,直到返回到更上级的调用(建议按Alt+B,关
闭所有中断):
经过三次返回,我们终于看到了关键点:
/*40193E*/ call crctest_.00401A80 // 这个调用进行自校验
/*401943*/ test al, al // 检查校验的结果
/*401945*/ jnz shortcrctest_.0040196F//如果通过就跳走
/*401947*/ mov eax,dwordptrds:[46EF94]
/*40194C*/ push 40010
/*401951*/ mov ecx,crctest_.0046A5E0
/*401956*/ mov edx,crctest_.0046A5BC
/*40195B*/ mov eax,dwordptrds:[eax]
/*40195D*/ call crctest_.00468C08
/*401962*/ mov edx,dwordptrds:[46EF94]
/*401968*/ mov eax,dwordptrds:[edx]
/*40196A*/ call crctest_.004488FC
/*40196F*/ mov edx,[local.10]//通过以后,就跳到这里
/*401972*/ mov dwordptrfs:[0],edx
/*401979*/ mov eax,[local.1]
/*40197C*/ test bl, bl
/*40197E*/ je shortcrctest_.00401985
/*401980*/ call crctest_.00468F61
/*401985*/ pop esi
/*401986*/ pop ebx
/*401987*/ mov esp,ebp
/*401989*/ pop ebp
/*40198A*/ retn
很显然,我们只要将00401945 处的代码:
jnzshortcrctest_.0040196F
修改为:jmpshortcrctest_.0040196F//强行跳转
就可以强制为自校验通过的状态。好了,接下来的保存工作就不用我多说了。最后,再用Keymake软件制作出破解补丁就可以完成注册了!软件包中就保存了破解补丁
crctest_patch.exe,大家只要运行就可以看到效果了!
OK,到目前为止,我为您制作的CRC保护实际已经被完全破解了,整个过程比较啰嗦,只是力求详尽。在看过这一部分后,您应该对破解CRC保护的软件有了感性和理性的认识。
附表1
CRC-16 的码表
dw 00000h,0C0C1h,0C181h,00140h,0C301h,003C0h,00280h,0C241h
dw 0C601h,006C0h,00780h,0C741h,00500h,0C5C1h,0C481h,00440h
dw 0CC01h,00CC0h,00D80h,0CD41h,00F00h,0CFC1h,0CE81h,00E40h
dw 00A00h,0CAC1h,0CB81h,00B40h,0C901h,009C0h,00880h,0C841h
dw 0D801h,018C0h,01980h,0D941h,01B00h,0DBC1h,0DA81h,01A40h
dw 01E00h,0DEC1h,0DF81h,01F40h,0DD01h,01DC0h,01C80h,0DC41h
dw 01400h,0D4C1h,0D581h,01540h,0D701h,017C0h,01680h,0D641h
dw 0D201h,012C0h,01380h,0D341h,01100h,0D1C1h,0D081h,01040h
dw 0F001h,030C0h,03180h,0F141h,03300h,0F3C1h,0F281h,03240h
dw 03600h,0F6C1h,0F781h,03740h,0F501h,035C0h,03480h,0F441h
dw 03C00h,0FCC1h,0FD81h,03D40h,0FF01h,03FC0h,03E80h,0FE41h
dw 0FA01h,03AC0h,03B80h,0FB41h,03900h,0F9C1h,0F881h,03840h
dw 02800h,0E8C1h,0E981h,02940h,0EB01h,02BC0h,02A80h,0EA41h
dw 0EE01h,02EC0h,02F80h,0EF41h,02D00h,0EDC1h,0EC81h,02C40h
dw 0E401h,024C0h,02580h,0E541h,02700h,0E7C1h,0E681h,02640h
dw 02200h,0E2C1h,0E381h,02340h,0E101h,021C0h,02080h,0E041h
dw 0A001h,060C0h,06180h,0A141h,06300h,0A3C1h,0A281h,06240h
dw 06600h,0A6C1h,0A781h,06740h,0A501h,065C0h,06480h,0A441h
dw 06C00h,0ACC1h,0AD81h,06D40h,0AF01h,06FC0h,06E80h,0AE41h
dw 0AA01h,06AC0h,06B80h,0AB41h,06900h,0A9C1h,0A881h,06840h
dw 07800h,0B8C1h,0B981h,07940h,0BB01h,07BC0h,07A80h,0BA41h
dw 0BE01h,07EC0h,07F80h,0BF41h,07D00h,0BDC1h,0BC81h,07C40h
dw 0B401h,074C0h,07580h,0B541h,07700h,0B7C1h,0B681h,07640h
dw 07200h,0B2C1h,0B381h,07340h,0B101h,071C0h,07080h,0B041h
dw 05000h,090C1h,09181h,05140h,09301h,053C0h,05280h,09241h
dw 09601h,056C0h,05780h,09741h,05500h,095C1h,09481h,05440h
dw 09C01h,05CC0h,05D80h,09D41h,05F00h,09FC1h,09E81h,05E40h
dw 05A00h,09AC1h,09B81h,05B40h,09901h,059C0h,05880h,09841h
dw 08801h,048C0h,04980h,08941h,04B00h,08BC1h,08A81h,04A40h
dw 04E00h,08EC1h,08F81h,04F40h,08D01h,04DC0h,04C80h,08C41h
dw 04400h,084C1h,08581h,04540h,08701h,047C0h,04680h,08641h
dw 08201h,042C0h,04380h,08341h,04100h,081C1h,08081h,04040h
附表2
CRC-32 的码表
dd000000000h,077073096h,0EE0E612Ch,0990951BAh,0076DC419h,0706AF48Fh,0E963A535h,09E6495A3h,00EDB8832h,079DCB8A4h
dd0E0D5E91Eh,097D2D988h,009B64C2Bh,07EB17CBDh,0E7B82D07h,090BF1D91h,01DB71064h,06AB020F2h,0F3B97148h,084BE41DEh
dd01ADAD47Dh,06DDDE4EBh,0F4D4B551h,083D385C7h,0136C9856h,0646BA8C0h,0FD62F97Ah,08A65C9ECh,014015C4Fh,063066CD9h
dd0FA0F3D63h,08D080DF5h,03B6E20C8h,04C69105Eh,0D56041E4h,0A2677172h,03C03E4D1h,04B04D447h,0D20D85FDh,0A50AB56Bh
dd035B5A8FAh,042B2986Ch,0DBBBC9D6h,0ACBCF940h,032D86CE3h,045DF5C75h,0DCD60DCFh,0ABD13D59h,026D930ACh,051DE003Ah
dd0C8D75180h,0BFD06116h,021B4F4B5h,056B3C423h,0CFBA9599h,0B8BDA50Fh,02802B89Eh,05F058808h,0C60CD9B2h,0B10BE924h
dd02F6F7C87h,058684C11h,0C1611DABh,0B6662D3Dh,076DC4190h,001DB7106h,098D220BCh,0EFD5102Ah,071B18589h,006B6B51Fh
dd09FBFE4A5h,0E8B8D433h,07807C9A2h,00F00F934h,09609A88Eh,0E10E9818h,07F6A0DBBh,0086D3D2Dh,091646C97h,0E6635C01h
dd06B6B51F4h,01C6C6162h,0856530D8h,0F262004Eh,06C0695EDh,01B01A57Bh,08208F4C1h,0F50FC457h,065B0D9C6h,012B7E950h
dd08BBEB8EAh,0FCB9887Ch,062DD1DDFh,015DA2D49h,08CD37CF3h,0FBD44C65h,04DB26158h,03AB551CEh,0A3BC0074h,0D4BB30E2h
dd04ADFA541h,03DD895D7h,0A4D1C46Dh,0D3D6F4FBh,04369E96Ah,0346ED9FCh,0AD678846h,0DA60B8D0h,044042D73h,033031DE5h
dd0AA0A4C5Fh,0DD0D7CC9h,05005713Ch,0270241AAh,0BE0B1010h,0C90C2086h,05768B525h,0206F85B3h,0B966D409h,0CE61E49Fh
dd05EDEF90Eh,029D9C998h,0B0D09822h,0C7D7A8B4h,059B33D17h,02EB40D81h,0B7BD5C3Bh,0C0BA6CADh,0EDB88320h,09ABFB3B6h
dd003B6E20Ch,074B1D29Ah,0EAD54739h,09DD277AFh,004DB2615h,073DC1683h,0E3630B12h,094643B84h,00D6D6A3Eh,07A6A5AA8h
dd0E40ECF0Bh,09309FF9Dh,00A00AE27h,07D079EB1h,0F00F9344h,08708A3D2h,01E01F268h,06906C2FEh,0F762575Dh,0806567CBh
dd0196C3671h,06E6B06E7h,0FED41B76h,089D32BE0h,010DA7A5Ah,067DD4ACCh,0F9B9DF6Fh,08EBEEFF9h,017B7BE43h,060B08ED5h
dd0D6D6A3E8h,0A1D1937Eh,038D8C2C4h,04FDFF252h,0D1BB67F1h,0A6BC5767h,03FB506DDh,048B2364Bh,0D80D2BDAh,0AF0A1B4Ch
dd036034AF6h,041047A60h,0DF60EFC3h,0A867DF55h,0316E8EEFh,04669BE79h,0CB61B38Ch,0BC66831Ah,0256FD2A0h,05268E236h
dd0CC0C7795h,0BB0B4703h,0220216B9h,05505262Fh,0C5BA3BBEh,0B2BD0B28h,02BB45A92h,05CB36A04h,0C2D7FFA7h,0B5D0CF31h
dd02CD99E8Bh,05BDEAE1Dh,09B64C2B0h,0EC63F226h,0756AA39Ch,0026D930Ah,09C0906A9h,0EB0E363Fh,072076785h,005005713h
dd095BF4A82h,0E2B87A14h,07BB12BAEh,00CB61B38h,092D28E9Bh,0E5D5BE0Dh,07CDCEFB7h,00BDBDF21h,086D3D2D4h,0F1D4E242h
dd068DDB3F8h,01FDA836Eh,081BE16CDh,0F6B9265Bh,06FB077E1h,018B74777h,088085AE6h,0FF0F6A70h,066063BCAh,011010B5Ch
dd08F659EFFh,0F862AE69h,0616BFFD3h,0166CCF45h,0A00AE278h,0D70DD2EEh,04E048354h,03903B3C2h,0A7672661h,0D06016F7h
dd04969474Dh,03E6E77DBh,0AED16A4Ah,0D9D65ADCh,040DF0B66h,037D83BF0h,0A9BCAE53h,0DEBB9EC5h,047B2CF7Fh,030B5FFE9h
dd0BDBDF21Ch,0CABAC28Ah,053B39330h,024B4A3A6h,0BAD03605h,0CDD70693h,054DE5729h,023D967BFh,0B3667A2Eh,0C4614AB8h
dd05D681B02h,02A6F2B94h,0B40BBE37h,0C30C8EA1h,05A05DF1Bh,02D02EF8Dh
|
| |||
|

评论