最近想利用条件随机场做一些实验。理论基础知识花了我一个星期时间。然后下载了CRF++的代码看看，又花了差不多一个星期。总算是把算法描述的东西和程序里的描述对应起来。

但是，这次学习的过程给我最大的感受就是网上关于这方面的知识还是偏少，尤其是关于CRF++代码的解释就更少了。由于CRF++本身的代码没有任何的注释，而很多函数动辄十几个参数，刚开始连参数代表什么意思，对应到算法描述中的什么变量都不知道。

这里，为了给这次学习过程一个总结，也为了给后面学习CRF，特别是使用CRF++代码的朋友们一个方便。

本文分两部分来描述，第一部分介绍算法原理，这里介绍的原理就是CRF++中用到的算法。 第二部分就是分析CRF++代码，介绍如何通过代码来实现这些算法。

 

一。 CRF原理

1．无约束最优化
　　对无约束最优化不熟悉的读者也许要问，什么是无约束最优化。这里以一个例子来说明该问题。
　　
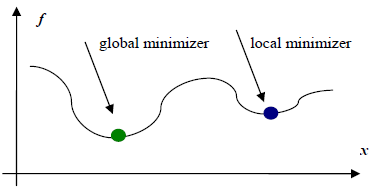
　　上图所示为一元函数f(x)的图像，无约束最优化问题，即不对定义域或值域做任何限制的情况下，求解函数f(x)的最小值，上面显示两个最小值点：一个为全局最小值点，另一个为局部最小值点。受限于算法复杂度等问题，目前大部分无约束最优化算法只能保证求取局部最小值点。这时读者不免要问，既然只能求取局部最小值点，那为什么这类算法还能应用呢。这是因为实际应用中，许多情形被抽象为函数形式后均为凸函数，对于凸函数来说局部最小值点即为全局最小值点，因此只要能求得这类函数的一个最小值点，该点一定为全局最小值点。
　　理解了上面的无约束最优化问题之后，我们就可以开始介绍无约束最优化的求解过程了，对于无约束最优化的求解首先我们需要选择一个初始点x_0，如下所示：
　　
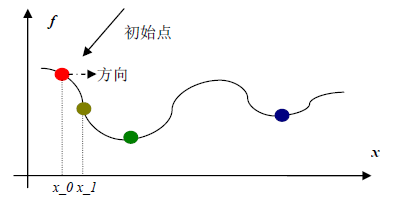
　　初始点选择好之后，就可以按照各种不同的无约束最优化求解算法，求解最小值点了。求解过程中主要涉及两个概念，即从初始点开始沿“哪个方向”以及“走多远”到达下一个点处。所谓“走多远”即之前提的“步长”的概念，“哪个方向”即方向概念。

 

2．Line Search
　　Line search主要用于解决之前提到的步长的概念，即方向确定好之后，需要确定从当前点x_k沿着该方向走多远，以便走到下一个合适的点x_k+1。若用p_k代表从第k个点走向第k+1点的方向，x_k代表当前点，x_k+1代表下一个点，a_k代表步长，则存在如下的等式：

　　x_k+1 = x_k + a_k * p_k　　　　　(1)

　　这里简要介绍一下p_k，大部分line search方法要求p_k为下降方向，即从当前点沿着p_k方向移动后导致函数值减少。由于目标是求取一个函数的最小值，因此最优的情况是求取沿p_k方向满足f(x_k+1)为全局最小的a_k值，可用下式表示为：

　　Ø (a_k) = f(x_k+1) = f(x_k + a_k * p_k) (2)

　　
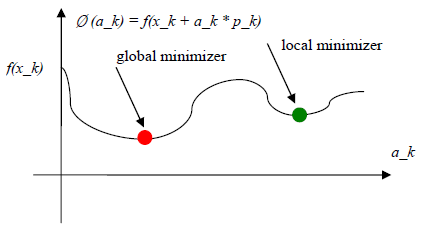
　　由于直接求取满足Ø (a_k)为全局最小值的a_k涉及到大量f(x_k + a_k * p_k)的计算，若从求导角度计算最小值，还会涉及到▽f_k+1的计算，计算量较大。因此从计算量角度考虑，可以采用如下较为折中的策略。
　　方向确定好之后，每一步的line Search主要涉及两个问题：1）什么样的a_k是合理的 2）如何选择a_k的长度。下面将沿这两个面展开讨论，首先讨论“什么样的a_k是合理的”，确定了该问题之后，我们就可以在此基础上选择a_k了。

2.1 a_k合理性讨论
　　如下将要讨论关于a_k需要满足的两个条件，当a_k满足这两个条件后，就可以认为从x_k点移动到x_k+1点的步长已经确定下来了。第一个条件为sufficient decrease condition，从直观角度来看，该条件主要要用保证x_k+1点的函数值要小于x_k点的函数值，满足该条件后，才有全局收敛 的可能性。第二个条件为curvature condition，从直观角度来看，该条件主要用于保证x_k点经过步长a_k的移动到达x_k+1后，▽f_k+1小于▽f_k。

2.1.1 sufficient decrease condition
　　a_k的选择一定要使得函数值满足sufficient decrease condition，该条件可以用如下不等式描述：
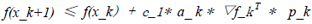　　 　　(3)
将公式（1）代入上式，可得：
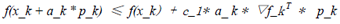　　 　　(4)
这里有必要对上面的不等式做一些解释：
　a) f(x_k) 代表函数在第x_k点的值
　b) ▽f_k代表函数在第x_k点的梯度
　c) p_k代表从第x_k点的走到x_k+1点的方向
　d) a_ k代表从第x_k点沿着p_k方向走到x_k+1点步长
　e) c_1为常量，需满足 0< c_1 < 1，一般取c_1为1E-4(注：Quasi-Newton Method中要求0< c_1< 0.5)
当p_k为函数下降方向时，有：

　　　　　 ▽f_k * p_k < 0 　　　　　 (5)

因此不等式4，即要求：

　　　　　　f(x_k+1) ＜ f(x_k) 　　　　　(6)

　　从图形角度看，函数位于第k点时，以上各参数中只有a_k为变量，其他均为常量，因此(4)可以用以下不等式重新描述为：

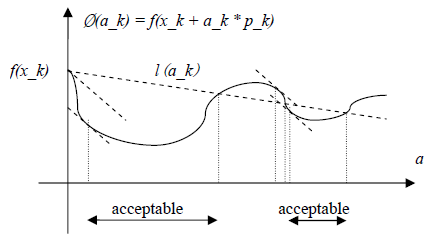
　　　　　　Ø(a_k) ≤ l(a_k) 　　　　　(7)

其中：
　　
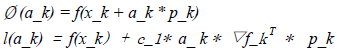
以下为不等式（7）的图形化表示：
　
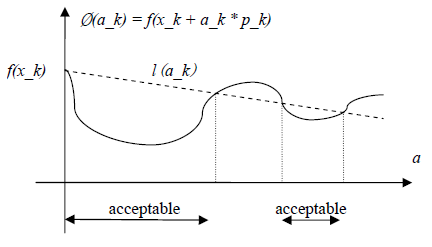
因此只要步长a_k的选择使得函数Ø(a_k)位于acceptable区间，就满足sufficient decrease condition。

2.1.2 curvature condition
　　a_k的选择一定要使得函数梯度值满足curvature condition，该条件可以用如下不等式描述：
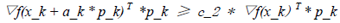　　 　　　 (8)
即为
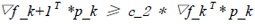　　　 　　 (9)
这里有必要对上面的不等式做一些解释：
　a) ▽f_k+1代表函数在第x_k+1点的梯度
　b) ▽f_k代表函数在第x_k点的梯度
　c) p_k代表从第k点的走到k+1点的方向
　d) c_2为常量，需满足0< c_1 < c_2 < 1，一般取c_2为0.9
当p_k为函数下降方向时，有：

　　　　　▽f_k * p_k < 0

因此不等式9，即要求：

　　　　　 ▽f _k+1 ≥ c_2 * ▽f_k 　　　　　　(10)

从图形角度看，不等式10即要求函数在第x_k+1点的变化速度要低于x_k点的变化速度，这一点可以从这两点处的梯度处看出，如下图所示。
　　

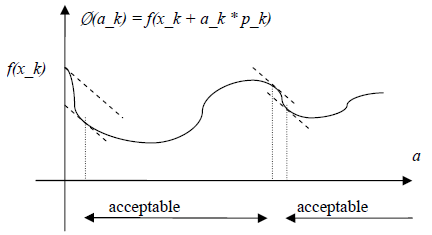
2.1.3 Wolfe conditions
　　所谓Wolfe conditions即sufficient decrease condition和curvature condition的综合，即a_k需要同时满足如下两个条件：
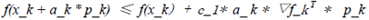　 (11)
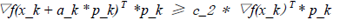　 (12)
图形化表示后，如下图所示：
　
实际应用中，常常会用到由Wolfe conditions引申出的strong Wolfe conditions，即a_k需要同时满足如下两个条件：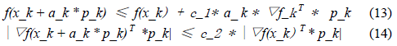
与Wolfe condtions唯一的区别是strong Wolfe condtions避免了▽f(x_k + a_k * p_k)取较大的正值情况。

2.2 a_k步长的选择
　　了解了a_k的合理性之后，就相当于获得了标尺，在此基础上我们可以选择合适的策略来求取a_k。所有的line search过程在计算每一步的a_k时，均需要提供一个初始点a_0，然后再此基础上生成一系列的{a_i}，直到a_i满足2.1节所规定的条件为止，此时该a_k即被确定为a_i，或者未找到一个合适的a_k。这里我们仅介绍目前常用的策略平方插值和立方插值法。因此本节内容分为两部分，2.2.1节介绍选择a_k常用的平方插值和立方插值法，2.2.2节介绍由x_k点到x_k+1点，方向确定为p_k后，步长a_k具体计算过程。

2.2.1 平方立方插值法
　　当给定一个初始步长a_0，若该初始步长满足Wolfe conditions（或strong Wolfe conditions），则a_k被确定为a_0，当前点x_k步长计算过程结束，否则，我们可以在此基础上，利用已知的三个信息Ø(a_0)、Ø(0)、Ø’(0)，构建一个二次（平方）插值多项式来拟合Ø(a_k)。该二次插值多项式如下所示：
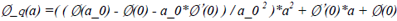(15)
观察上面的二次插值多项式可知，其满足如下插值条件：

Ø_q(0) = Ø(0)　Ø_q’(0) = Ø’(0)　Ø_q(a_0) = Ø(a_0)

对二次插值多项式(15)求导并令其为零，即可获得使得该多项式取得最小值的a值，如下所示：
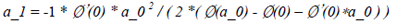(16)
若a_1满足Wolfe conditions（或strong Wolfe conditions），则a_k 被确定为a_1。否则在此基础上构建一个三次（立方）插值多项式，并求得使得该多项式取最小值的a值，该a值的计算公式如下所示：

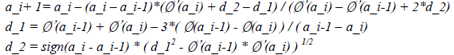
　　　　　　　　　　　　　　　　　　　　　　　　　　　(17)
若a_i+1满足Wolfe conditions（或strong Wolfe conditions），则a_k 被确定为a_i+1，否则一直使用三次插值多项式进行插值拟合。并且选择使用a_i+1对应的Ø (a_i+1)和Ø’(a_i+1)替换a_i-1或a_i相应的值，一旦确定好a_i-1或a_i中的一种后，每次都替换对应的值，如替换a_i-1，则每次都使用新的a_i+1对应的值替换a_i-1，直到找到满足Wolfe conditions（或strong Wolfe conditions）的a_i+1为止，此时a_k被确定为a_i+1，或者没有找到合适的a_i+1。
　　这里有必要简略解释一下为何只使用到三次插值多项式，而没有使用更高阶的插值多项式。原因是三次插值多项式对函数某个点处的具体值有较好的拟合效果，同时又有较好的抗过拟合作用。
　　最后有必要解释一下初始步长a_0的选择，对于Newton或quasi-Newton methods来说，初始步长a_0总是确定为1，该选择确保当满足Wolfe conditions（或strong Wolfe conditions），我们总是选择单位1步长，因为该步长使得Newton或quasi-Newton methods达到较快的收敛速度。计算第零步长时，将初始步长a_0使用如下公式确定：
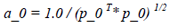　　　　　 (18)
第1步及其以后的初始步长a_0，直接设定为1。

2.2.2 步长a_k计算
　　本节主要做一个总结，即综合前面步长需要满足的条件及步长迭代计算公式给出步长计算的具体过程。下面假设我们处于x_k点，因此要从该点选择一个满足Wolfe (或strong Wolfe) conditions的步长a_k，以便走到下一点x_k+1。因此我们选择初始点a_0 = 1，Newton或quasi-Newton method中初始步长总是选择为1。因此有：

1) 初始化 a_xa_y0 Ø(a_x) 、 Ø(a_y) 、Ø’(a_x) 、 Ø’(a_y)、a_min、a_max
2) 初始化 a_ia_0、Ø’(a_i)、Ø(a_i)
3) 若Ø(a_i) > Ø(a_x)

　说明步长a_i选择的过大，因此使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_x和a_i之间，使用平方和立方插值法对a_x和a_i分别进行插值，求取两个新的步长a_quadratic和a_cubic，并取两者之中和a_x较接近的步长，这里假设为a_quadratic，将新的步长设为a_qudratic，同时进行以下操作：

a_y a_i
Ø(a_y) Ø(a_i)
Ø’(a_y) Ø’(a_i)
a_i+1 a_quadrati

同时在此情况下，说明a_k位于a_x和a_y之间

4) 若Ø’(a_i)* Ø’(a_x) < 0
　　说明步长a_i选择的过大，因此使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_x和a_i之间，使用平方和立方插值法对a_x和a_i分别进行插值，求取两个新的步长a_quadratic和a_cubic，并取两者之中和a_i较接近的步长，这里假设为a_quadratic，将新的步长设为a_qudratic，同时进行以下操作：

a_y a_x
Ø(a_y) Ø(a_x)
Ø’(a_y) Ø’(a_x)

a_x a_i
Ø(a_x) Ø(a_i)
Ø’(a_x) Ø’(a_i)

a_i+1 a_quadrati

同时在此情况下，说明a_k位于a_x和a_y之间

5) 若|Ø’(a_i)| <|Ø’(a_x) |
　　说明步长a_i选择的过小，因此使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_i和a_y之间，使用平方和立方插值法对a_x和a_i分别进行插值，求取两个新的步长a_quadratic和a_cubic，并取两者之中和a_i较接近的步长，这里假设为a_quadratic，将新的步长设为a_qudratic，同时进行以下操作：

a_x a_i
Ø(a_x) Ø(a_i)
Ø’(a_x) Ø’(a_i)

a_i+1 a_quadrati

同时在此情况下，说明a_k位于a_x和a_y之间

6) 若|Ø’(a_i)| ≥|Ø’(a_x) |
　　说明步长a_i选择的过小，若之前已经确定出了a_k所属的范围a_x和a_y，则使得Ø(a_i)满足Wolfe(或strong Wolfe) conditions的步长a_k应位于a_i和a_y之间，使用立方插值法对a_i和a_y进行插值，求取新的步长a_cubic，新的步长设为a_cubic；否则若a_x小于a_i，说明的新的步长不够大，因此将新的步长设置为a_max，若a_x大于等于a_i，则说明新的步长不够小，将其设为a_min，同时进行以下操作：

a_x a_i
Ø(a_x) Ø(a_i)
Ø’(a_x) Ø’(a_i)

if 之前已经确定出了a_k所属的范围a_x和a_y

a_i+1 a_cubic
else if a_x ＜ a_i
a_i+1 a_max
else if a_x ≥ a_i
a_i+1 a_min

7) 计算判断若a_i+1使得以下两式(strong Wolfe condition)均成立：

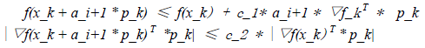
则找到合理的步长a_k，将其设定为a_i+1

a_k a_i+1

则x_k点步长a_k计算结束。
否则转到2）继续计算合理步长。

 

3．Quasi-Newton Method
　　在第2节中我们了解了步长的概念，以及从x_k走到x_k+1点使用line search方法计算步长的方法。不过我们在那里忽略了一个重要的概念，即“方向”。从第2节，我们了解到从每一点x_k走到下一点x_k+1时，需要给出要走的“方向”，只有“方向”确定好之后，才能在此基础上应用line search方法找到对应的“步长”，因此在解决了“步长”计算问题之后，这里我们将和大家一起了解一下每一步的“方向”如何确定。本节分为2大部分，首先我们通过newton method引入方向的概念，在此基础上引入quasi-newton method。然后引入quasi-newton method中的一种重要方法BFGS method，并在BFGS method的基础上介绍用于大规模计算的LBFGS method算法，同时以此结束本节的所有内容。

3.1 Newton Method
　　我想我们还依稀记得，微积分中用于求一元函数根的Newton法。该方法可用如下所示的图形来描述：

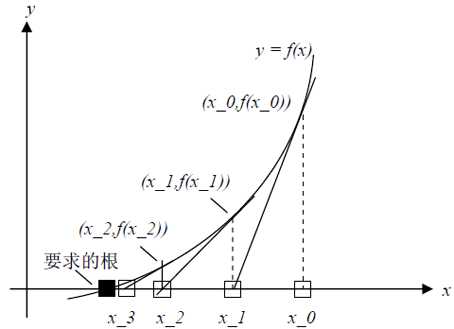
首先我们选择一个初始点x_0并计算获得其对应的f(x_0)，然后该方法用曲线y = f(x)在(x_0,f(x_0))的切线近似该曲线，把切线和x轴的交点记作x_1，点x_1通常x_0更接近所要求得根，同样方法用点x_1处的切线近似该曲线，并求取切线和x轴的交点x_2，一直迭代下去，直到找到满足我们所需的充分接近真实跟的解为止。因此Newton法从第k次近似值x_k求得第k+1次近似值x_k+1即为求x_k点处的切线和x轴的交点。
切线方程为：

y – f(x_k) = ▽f (x_k)(x – x_k)
=> 0 – f(x_k) =▽ f(x_k)(x – x_k)
=> ▽f(x_k)*x = ▽f(x_k)*x_k – f(x_k)
=> x = x_k – f(x_k)/▽f (x_k)

　　因此x_k+1 = x_k – f(x_k)/▽f(x_k) 　　　　　 (19)
　　从上面使用Newton Method求函数根的过程可以发现，首先需要选择一个初始点，并在点处构建一个模型来近似该函数。
　　切线模型：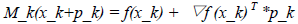
　　上面使用了相应点处的切线模型来近似函数，然后求取该近似模型的根以便求得更接近函数根的下一个点，该过程一直迭代下去，直到找到根为止。从上面构建每个点处的近似模型可以发现，该模型相对原函数来说简化了很多，因此求解要容易一些。
　　现在来考虑求取函数的最小值问题，方法类似。首先开始我们选择一个初始点x_0，并构建函数在该点处的一个近似模型，上面求函数根时，我们构建的近似模型为切线模型。这里我们构建一个抛物线模型：

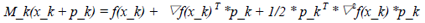
　　并求解该模型的梯度，同时令其为零，即：▽M_k(x+) = 0，在此基础上求得x+，该值即使得近似模型取得最小值的点。
　　对抛物线模型M_k求导并令其为零后，可得以下公式：
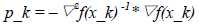　　　　　　　　　(20)
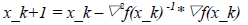　　因此 　　　　　(21)
　　从上式可见，使用Newton法时，每一步的方向为p_k，而步长为1。从Newton法方向公式我们不难看出，若使用Newton法，则从每个最小值近似点x_k走到下一个近似点x_k+1的过程中将涉及函数Hessian矩阵▽▽f(x_k) (二阶导)计算，而该Hessian矩阵无法保证在每个点处都是正定的，对正定矩阵来说存在如下不等式：
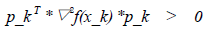　　　　　　　　　(22)
　　由于矩阵无法保证为正定矩阵，因此下式中
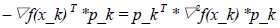　　　　　　　　　(23)
　　p_k无法保证总是为下降方向，即负梯度方向。
从上面的分析可见，Newton Method面临两个问题：
1) Hessian矩阵计算量较大
2) Hessian矩阵无法保证在迭代的过程中始终处于正定状态
为了解决这两个问题，我们引入Quasi-Newton Method。

 

3.2 Quasi-Newton Method
　　Quasi-Newton Method每一步计算过程中仅涉及到函数值和函数梯度值计算，这样有效避免了Newton Method中涉及到的Hessian矩阵计算问题。于Newton Method不同的是Quasi-Newton Method在每点处构建一个如下的近似模型：
　
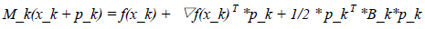
从上面的近似模型我们可以看出，该模型用B_k代替了Newton Method中近似模型中涉及到的Hessian矩阵。因此Quasi-Newton Method中方向计算公式如下所示：
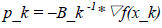　　　　　　　　　(24)
　　这里有必要解释一下用于近似Hessian矩阵的B_k可行性，及一个指导性方案。根据Taylor(泰勒)级数可知如下公式：

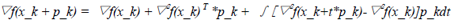
由于函数▽f(.)连续，因此上式可以表示为：

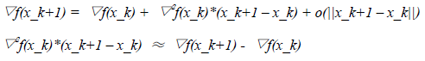
　　　　　　　　　　　　　　　　　　　　　　　　　　　(25)
　　因此每一选择Hessian矩阵的近似B_ k+1时，可以像式(24)那样模仿真实的Hessian矩阵的性质。得到下式：
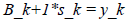　　　　　　　　　　(26)
其中：

s_k = x_k+1 – x_k　y_k = ▽f(x_k+1) – ▽f(x_k)　(27)

同时要求B_k+1为对称正定矩阵。

3.2.1 BFGS Method
　　从Quasi-Newton Method方向公式 (24) 中，可以看到每一步计算方向的过程中均涉及到B_k+1矩阵求逆的问题，为了避免该计算，通过分析公式（26）可知，我们可以构建一个近似H_k+1，该近视满足如下方程：

　　　H_k+1*y_k = s_k　　　　　(28)

同时要求H_k+1为对称正定矩阵。因此BFGS Method中，每个点处的方向由如下公式计算：

　　　p_k = –H_k*▽f(x_k)　　　(29)

　　在此基础上，BFGS方向迭代公式如下所示：

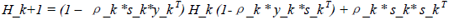
　　　　　　　　　　　　　　　　　　　　　　　　　(30)
其中ρ_k为一个标量：
　　　　　
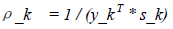
有了上面(30)的H_k迭代公式后，还有一个问题就是初始的H_0如何计算，目前常用的方法是初始的H_0直接设为单位矩阵I。因此BFGS Method用于解无约束最优化的过程可以表示为如下过程：

3.2.2 LBFGS Method
　　上一节所介绍的BFGS Method比较适合解决中小规模无约束最优化问题，但是BFGS算法产生的Hessian近似矩阵H_k为n * n的，同时该矩阵非稀疏，因此当n的规模较大时将面临两个问题：
1） 存储问题：n规模较大时，n*n矩阵对内存的消耗将较大；
2） 计算问题：n规模较大，同时n*n矩阵非稀疏时，计算复杂度将较高；
为了解决以上问题，引申出了Limited-Memory Quasi-Newton Method，目前使用较多的LBFGS算法即属于该类算法。为了减少H_k矩阵的存储，LBFGS算法利用最近几代的curvature 信息来构建Hessian矩阵的近似。由BFGS Method我们知道：

　　　x_k+1 = x_k + a_k * H_k*▽f(x_k)

其中a_k为步长，H_k为Hessian矩阵的近似，可以通过如下迭代公式计算：

　H_k+1 = V_k* H_k*V_k+ρ_k * s_k* s_k　　　(31)

其中：
　　
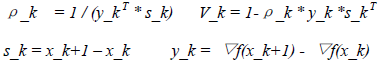
从上面的H_k的迭代计算公式可知，H_k会慢慢由稀疏矩阵转变为稠密矩阵，因此存储该矩阵以及进行该矩阵和向量的相乘运算的消耗将较大。为了避免该问题，LBFGS算法在BFGS算法的基础上从两点进行了改进：
1）估算每一步对应的Hessian近似矩阵时，给出一个当前步的初始Hessian矩阵估计H_k0
2) 利用过去当前代及过去m-1代的curvature信息修正初始Hessian矩阵估计H_k0，得到最终的Hessian矩阵近似估计H_k。
计算式如下所示：

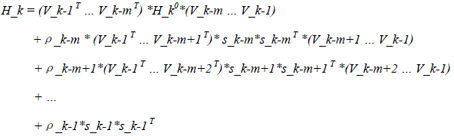
　　　　　　　　　　　　　　　　　　　　　(32)
上述计算式(32），可以通过公式(31)递归计算获取。公式(32)可以用以下算法表示：
　　　　　
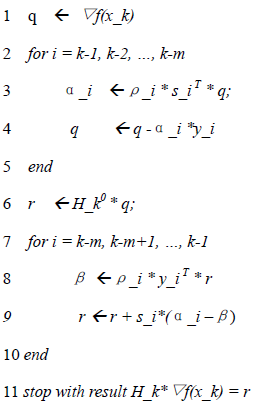
　　从上面计算H_k的公式(32)可知，要估算每个点x_k处的Hessian矩阵近似，需要给出初始估计H_k0，H_k0一般通过以下公式计算：
　　　　　
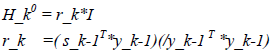
有了上面的方向计算算法后，LBFGS算法用于解无约束最优化问题，可以表示为如下算法：

1 选择一个初始点x_0，并选择收敛判断条件 ε> 0，以及常量m(代表过去代数)一般为6
2 k 0 H_0 I，因此r = H_0 *▽f(x_0) =▽f(x_0)
3 while ||▽f(x_k)|| > ε
4 　　计算从当前点x_k走到下一个点x_k+1的方向
　　　　　　p_k = –r
5 采用line search策略计算步长a_k
6 x_k+1 = x_k + a_k * p_k
7 if k > m
　　　删除LBFGS计算H_k时用不上的向量对(s_k-m, y_k-m)
8 计算并保存 s_k = x_k+1 – x_k y_k = ▽f(x_k+1) – ▽f(x_k)
9 采用LBFGS Hessian矩阵近似算法计算 r
10 k k+1

4．算法总结
　　用于解无约束优化算法的Quasi-Newton Method中的LBFGS算法到这里总算初步介绍完了，不过这里笔者要承认的是这篇文档省略了许多内容，包括算法收敛性的证明以及收敛速度证明等许多内容。因此读者若希望对这一块有一个更深入的认识可以参考以下两本书：
1) Numerical Methods for Unconstrained Optimization and Nonlinear Equations（J.E. Dennis Jr. Robert B. Schnabel）
2) Numerical Optimization（Jorge Nocedal Stephen J. Wright）

 

 

这里只是介绍了LBFGS来求解无约束最优化的问题的原理。 上述原理是引至我爱自然语言处理网的一篇文章，个人只是觉得这篇文章已经基本说清楚了无约束优化问题，以及后面要介绍的CRF的原理，故直接应用该文了。这里对这篇文章的原来作者表示非常的感谢。以下是这篇文章的原文地址：

http://www.52nlp.cn/unconstrained-optimization-one

 

未完，待续。后面主要介绍CRF实现及CRF++代码实现

评论

您需要登录后才能评论，请 登录 或者 注册